- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
                                                                                                                                                          16 January 1951

TO WHOM IT MAY CONCERN:
We the undersigned Rudell 0. BLANKENSHIP, Clarence A. SLOPER and Clifford L. GOODWIN this date 16 January 1951 have to our knowledge discovered the means of trisecting any angle with the use of a straight edge and compass only. The solution was arrived at in the following manner:

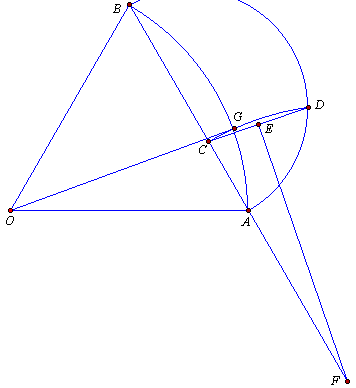
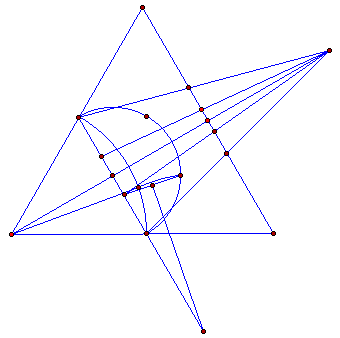
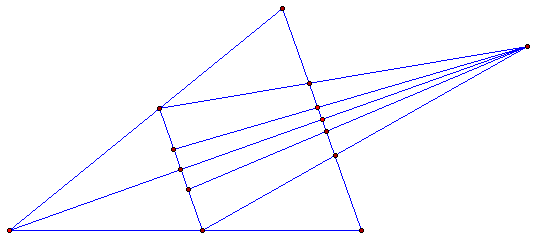
1. Bisect any angle with a line.

2. Construct a perpendicular to the bisecting line (intersecting both legs of the angle).

3. Construct a second perpendicular to the bisecting line further from
the apex.

4. Construct on the second perpendicular, a trisected line which is also bisected by the bisecting line.

5. Draw lines from the points of intersection (of the first perpendi­cular and the legs of the angle)through the outer points of the second trisected perpendicular, to a point on the bisecting line.

6. From this point draw lines through the points of trisection to pro­ject onto the first perpendicular to the bisecting line, thus trisecting the first perpendicular.

7. Draw a semi-circle whose diameter is formed by the segment of the first perpendicular to the bisecting line, between the legs of the angle.

8. Using the radius of this semi-circle, strike arcs trisecting the circumference of the semi-circle.

9. Draw a line connecting the point of trisection of the first perpendi­cular and the corresponding point of trisection of the semi-circle.

10. Bisect this line with a perpendicular and extend it to intersect with the first perpendicular to the first bisecting line.

l1. From this point of intersection, strike an arc which intersects the two corresponding points of trisection.

12. Using as a radius a distance from the apex of the angle to the point of intersection of one leg and the perpendicular to the first bisecting line; strick the arc of the angle to be trisected.

13. This arc will intersect the arc which passes through the two corresponding points of trisection, at the point of trisection of the arc of the angle to be trisected.

14. Using the chord of this trisection as a radius, strike off the two remaining and equal segments of the arc of the angle to be trisected.

- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -

15. Connect these points of trisection of the arc with the apex of the angle and the angle is trisected.

/s/ Rudell O. Blankenship                         /s/ Clarence A. Sloper                          /s Clifford L. Goodwin
RUDELL O. BLANKENSHIP                    CLARENCE A. SLOPER                        CLIFFORD L. GOODWIN

On January 16, 1951, we have personally witnessed Rudell O. BLANKENSHIP, Clarence A. SLOPER and Clifford L. GOODWIN work on, and to our knowledge, successfully completed the trisecting of angles with the use of the above method.
 

/s/ Carl E. Bolduc                                              /s/ R. Vaingat                             /s/ John W. Baillie
CARL E.BOLDUC                                          R. VAINGAT                                JOHN W. BAILLIE
 

STATE OF NEW YORK
COUNTY OF NIAGARA
CITY OF NIAGARA FALLS, N.Y.

Sworn to before me on this 17th day of January 1951

   /s/ Margaret Mary Garrow
             Notary Public

MARGARET MARY GARROW Reg. No. 1767
Notary Public, State of New York
Residing in Niagara County at time of appointment
Certificate filed in Erie County
My Commission Expires March 30, 1951